
Linear functions represent relationships where the rate of change is constant, often modeled by equations of the form y = mx + b. They are fundamental in algebra, describing straight lines graphically, with applications in economics, physics, and real-world problem-solving. Understanding linear functions is crucial for analyzing and predicting outcomes in various scenarios.
1.1 Definition of Linear Functions
A linear function is a mathematical relationship that can be expressed in the form f(x) = mx + b, where m represents the slope and b is the y-intercept. It is a polynomial function of degree one, meaning the highest power of the variable (usually x) is one. Linear functions graph as straight lines on a coordinate plane, with the slope m indicating the steepness and direction of the line. The y-intercept b is the point where the line crosses the y-axis. These functions are fundamental in algebra and are characterized by a constant rate of change between any two points on the line. They can also be represented in other forms, such as standard or point-slope form, depending on the context.
1.2 Importance of Linear Functions in Mathematics
Linear functions are foundational in mathematics, serving as the simplest form of functional relationships. They introduce key concepts like slope, y-intercept, and rate of change, which are essential for understanding more complex functions. Linear functions are used to model real-world phenomena, such as cost-benefit analysis or distance-time relationships, making them vital for problem-solving. They also form the basis for linear equations and systems, which are critical in various fields like economics, engineering, and physics. Additionally, linear functions are used in graphing and data analysis, providing a straightforward way to visualize and interpret relationships between variables. Their simplicity makes them a fundamental tool for teaching and applying mathematical principles across disciplines.
1.3 Real-World Applications of Linear Functions
Linear functions have numerous practical applications in everyday life and various professions. In finance, they are used to calculate interest rates, investment returns, and budget planning. In physics, linear functions model motion at constant speed and force. Engineers rely on them for designing structures and systems with predictable behavior. Economists use linear functions to understand supply-demand relationships and cost-benefit analysis. They are also essential in everyday problem-solving, such as calculating distance, time, and speed for travel. Linear functions provide a straightforward way to make predictions and informed decisions in fields like healthcare, education, and environmental science. Their simplicity makes them a versatile tool for real-world problem-solving.

Properties of Linear Functions
Linear functions are defined by their slope and y-intercept, which determine their steepness and positioning on a graph. They have a constant rate of change, ensuring straight-line graphs with a defined domain and range.
2.1 Slope of a Linear Function
The slope, denoted as m, measures the steepness of a linear function. It represents the change in the y-value per unit change in the x-value, calculated as m = (y2 ⏤ y1) / (x2 ⏤ x1). A positive slope indicates an upward trend, while a negative slope shows a downward trend. A zero slope means the function is constant, and an undefined slope signifies a vertical line. The slope is crucial for graphing and understanding the behavior of linear functions, as it determines the direction and steepness of the line. This property is essential in real-world applications, such as calculating rates of change in economics or physics.
2.2 y-intercept and Its Significance
The y-intercept, denoted as b in the equation y = mx + b, is the point where the graph of a linear function crosses the y-axis. It occurs when x = 0, making it a critical reference point for graphing. The y-intercept provides essential information about the function’s starting value and is often interpreted as the initial condition or baseline in real-world applications. For instance, in a cost-benefit analysis, the y-intercept might represent fixed costs before any production begins. Understanding the y-intercept is vital for accurately plotting linear functions and interpreting their practical implications in fields like economics, engineering, and science.
2.3 Domain and Range of Linear Functions
The domain of a linear function is the set of all possible input values (x-values) for which the function is defined. For most linear functions, the domain is all real numbers unless restricted by the context. The range, on the other hand, is the set of all possible output values (y-values) the function can produce. Since linear functions graph as straight lines, their domain and range are typically all real numbers, unless specific constraints are applied. Understanding the domain and range is essential for interpreting the behavior of linear functions in real-world scenarios, such as modeling growth rates or energy consumption, where restrictions may apply.

Equation of a Line
The equation of a line is a mathematical expression that describes a line’s graph. It is commonly expressed in slope-intercept, point-slope, or standard form, representing linear relationships effectively.
3.1 Slope-Intercept Form (y = mx + b)
The slope-intercept form of a line is expressed as y = mx + b, where m represents the slope and b is the y-intercept. This form is widely used because it directly provides the slope and the point where the line crosses the y-axis. The slope, m, indicates the steepness and direction of the line, while b gives the starting point of the line on the y-axis. For example, in the equation y = 2x + 3, the slope is 2, and the y-intercept is 3. This form is particularly useful for graphing lines and understanding their behavior. It simplifies identifying key features of linear functions, making it a foundational tool in algebra and analytics.
3.2 Point-Slope Form (y, y1 = m(x — x1))
The point-slope form, y — y1 = m(x — x1), is another way to express a linear equation. It is particularly useful when you know a point (x1, y1) that the line passes through and the slope m. This form is derived from the slope formula and is handy for writing the equation of a line when given a point and the slope. For instance, if a line has a slope of 3 and passes through the point (2, 4), the equation becomes y — 4 = 3(x ⏤ 2). This form is versatile and often used in calculus and analytic geometry for its adaptability in various mathematical scenarios.
3.3 Standard Form (Ax + By = C)
The standard form of a linear equation is Ax + By = C, where A, B, and C are integers, and A is non-negative. This form is particularly useful for identifying intercepts and coefficients in real-world applications. It is often preferred for systems of equations because it simplifies comparisons and substitutions. To convert from slope-intercept form, rearrange the equation to eliminate fractions and ensure A is positive. For example, y = 2x + 3 becomes 2x ⏤ y = 3. Standard form is also convenient for graphing, as it directly provides the x-intercept (C/A) and y-intercept (C/B) when applicable.
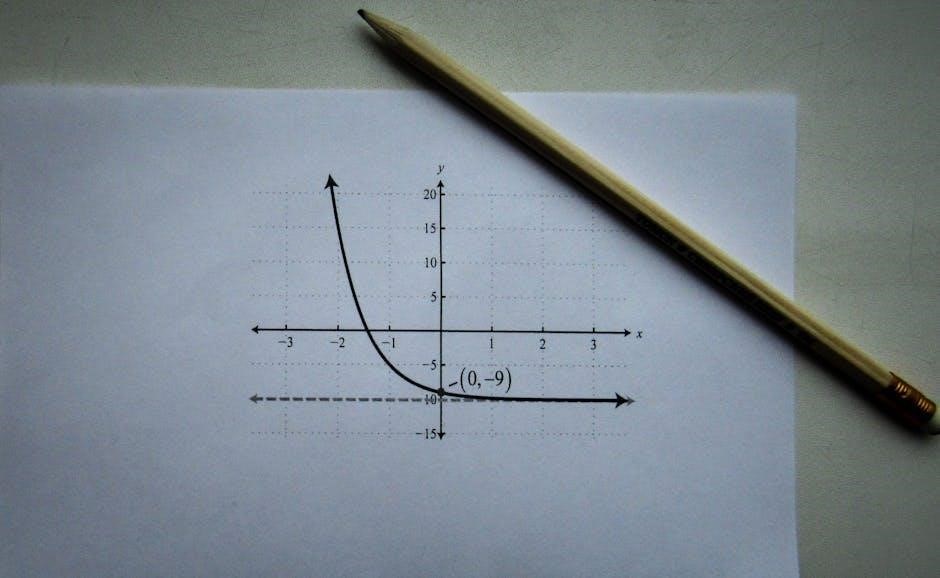
Graphing Linear Functions
Graphing linear functions involves plotting points and drawing straight lines. Use slope and y-intercept to identify key points, then connect them to form the line accurately.
4.1 Plotting Points to Graph a Line
Plotting points is a foundational step in graphing linear functions. Begin by identifying two or more points from the equation, such as the y-intercept and another point derived by plugging in a value for x. Mark these points accurately on the graph, ensuring they align with the grid lines. Once plotted, connect the points with a straight line using a ruler to maintain accuracy. This method works for any linear equation, as it relies on the function’s constant rate of change. Always double-check the coordinates of your points to avoid errors. Plotting multiple points helps confirm the line’s direction and slope, making the graph clear and precise for analysis.
4.2 Using Slope and y-intercept to Graph a Line
Graphing a line using slope and y-intercept is a straightforward method. Start by identifying the y-intercept, b, from the equation y = mx + b. Plot this point on the y-axis. Next, use the slope, m, to determine the line’s steepness and direction. A positive slope rises from left to right, while a negative slope falls. Move m units up or down for every 1 unit moved to the right. Plot a second point and draw a straight line through both points. Extend the line in both directions and add arrows to indicate it continues indefinitely. This method ensures accuracy and clarity in visualizing the linear relationship defined by the equation.
4.3 Identifying Intercepts from a Graph
Identifying intercepts from a graph is essential for understanding linear functions. The y-intercept occurs where the line crosses the y-axis (where x = 0). To find it, locate the point on the graph where the line intersects the y-axis and note the y-value. The x-intercept occurs where the line crosses the x-axis (where y = 0). To find it, locate the point where the line intersects the x-axis and note the x-value. These intercepts provide key information about the line’s equation and behavior. For example, the y-intercept gives the value of b in the slope-intercept form y = mx + b, while the x-intercept helps identify roots or solutions to the equation.

Systems of Linear Equations
A system of linear equations consists of two or more equations with the same variables, allowing for the simultaneous determination of variable values that satisfy all equations.
5.1 Definition of a System of Equations
A system of linear equations is a collection of two or more linear equations that share the same set of variables. These equations work together to find values for the variables that satisfy all equations simultaneously. For example, a system might consist of equations like y = 2x + 3 and y = x ⏤ 1. Solving such systems helps determine the point where the equations intersect, providing a solution that applies to all equations in the system. Systems of equations are widely used in real-world applications, such as resource allocation, cost analysis, and physics problems, where multiple conditions must be satisfied.
5.2 Types of Solutions: Consistent, Inconsistent, and Dependent Systems
A system of equations can have three types of solutions: consistent, inconsistent, or dependent; A consistent system has exactly one solution, where the lines intersect at a single point. An inconsistent system has no solution, occurring when the lines are parallel and do not intersect. A dependent system has infinitely many solutions, as the equations represent the same line. These classifications are determined by comparing the slopes and y-intercepts of the equations. Graphically, consistent systems cross at one point, inconsistent systems run parallel, and dependent systems overlap completely. Understanding these types is crucial for solving and interpreting linear systems in various applications.
5.3 Graphical Representation of Systems of Equations
Graphically, a system of equations can be represented by plotting the lines corresponding to each equation on a coordinate plane. The solution to the system is the point where the lines intersect. For consistent systems, the lines intersect at one unique point, representing a single solution. Inconsistent systems result in parallel lines that never intersect, indicating no solution. Dependent systems occur when the lines are identical, meaning there are infinitely many solutions. Graphing provides a visual method to identify the type of system and its solution set. This approach is particularly useful for understanding relationships between variables and verifying solutions obtained algebraically.
Solving Systems of Linear Equations
Solving systems of linear equations involves finding values that satisfy all equations simultaneously. Common methods include substitution, elimination, and graphical approaches. Each method ensures accuracy and efficiency in finding solutions.
6.1 Substitution Method
The substitution method involves solving one equation for a variable and substituting it into the other equation. This eliminates one variable, allowing for solving the remaining equation. For example, if you have equations ( y = 2x + 3 ) and ( 3x + 2y = 7 ), you can substitute ( y ) from the first equation into the second, resulting in ( 3x + 2(2x + 3) = 7 ). Simplifying this gives ( 7x + 6 = 7 ), leading to ( x = rac{1}{7} ). Substituting ( x ) back into the first equation yields ( y = 2( rac{1}{7}) + 3 = rac{23}{7} ). This method is effective for systems where one equation is easily solvable for a variable.
6.2 Elimination Method
The elimination method involves manipulating two equations to eliminate one variable by adding or subtracting them. To do this, the coefficients of the variable to be eliminated must be made equal. For example, consider the system:
3x + 4y = 11
2x + 4y = 7
Subtract the second equation from the first:
(3x + 4y) ⏤ (2x + 4y) = 11 — 7
This simplifies to:
x = 4
Substitute ( x = 4 ) back into one of the original equations to find ( y = 1 ). This method is efficient when the coefficients of a variable in both equations are the same or can easily be made equal. It avoids the need to solve for one variable explicitly, streamlining the process.
6.3 Special Cases in Systems of Equations
Special cases in systems of equations arise when the equations are either dependent or inconsistent. A dependent system occurs when the two equations represent the same line, resulting in infinitely many solutions. For example, the system:
2x + 4y = 8
x + 2y = 4
are multiples of each other, indicating all points on the line satisfy both equations. An inconsistent system has no solution, as the lines are parallel and never intersect. For instance:
y = 2x + 3
y = 2x + 5
These cases highlight the importance of analyzing coefficients and constants to determine the system’s behavior.
Linear Inequalities
Linear inequalities involve expressions with variables and inequality signs (<, >, ≥, ≤). They are solved similarly to equations but require careful handling when multiplying or dividing by negatives. Essential for modeling real-world constraints, such as budgeting or resource allocation, they extend the principles of linear equations to compare ranges of values.
7.1 Solving One-Variable Linear Inequalities
A one-variable linear inequality involves a single variable and an inequality sign (<, >, ≤, ≥). To solve, simplify the expression by performing operations like addition, subtraction, multiplication, or division. The goal is to isolate the variable on one side. When multiplying or dividing by a negative number, the inequality sign must be reversed. For example, solving 2x + 3 ≤ 5 involves subtracting 3 from both sides, resulting in 2x ≤ 2, then dividing by 2 to find x ≤ 1. Graphing solutions on a number line helps visualize the range of valid values. Always check if the solution satisfies the original inequality.
7.2 Graphing Linear Inequalities on a Number Line
Graphing linear inequalities on a number line involves representing the solution set visually. Start by identifying the critical point from the inequality, such as x = 3 for x ≤ 3. Mark this point on the number line. If the inequality is strict (< or >), use an open circle; if it includes equality (≤ or ≥), use a closed circle. Draw an arrow to indicate the direction of the solution set. For example, x < 4 would show an open circle at 4 with an arrow extending to the left. Always test a point in the solution range to confirm the inequality direction. This method helps visualize the range of values that satisfy the inequality.
7.3 Solving Compound Linear Inequalities
Compound linear inequalities involve two or more inequalities combined with “and” or “or.” For “and” conditions, the solution is the overlap of both inequalities. For example, 2x + 3 ≥ 5 and x ⏤ 2 < 4 requires solving each separately: x ≥ 1 and x < 6, resulting in 1 ≤ x < 6. For "or" conditions, the solution includes all values satisfying either inequality. Testing points in each interval helps determine the correct intervals. Graphing compound inequalities on a number line involves shading the appropriate regions and checking endpoints. This method ensures clarity in identifying the combined solution set for complex inequalities.

Applications of Linear Systems
Linear systems are essential in real-world problem-solving, such as budgeting, resource allocation, and optimization. They model scenarios like cost-benefit analysis, distance-speed-time problems, and economic forecasting, providing practical solutions.
8.1 Word Problems Involving Linear Systems
Word problems involving linear systems often require interpreting real-life scenarios into mathematical equations. Common examples include budget planning, where total expenses and income form a system, and mixture problems, like combining solutions with different concentrations. These problems typically involve two or more variables and require setting up a system of equations to solve. For instance, determining the number of hours two people need to complete a task together, given their individual rates, is a classic application. Once the system is defined, methods like substitution or elimination can be applied to find the solution. Real-world context makes these problems practical and relevant.
8.2 Cost and Revenue Models
Cost and revenue models are essential tools for businesses to predict financial outcomes. These models often utilize linear functions to represent the relationship between costs incurred and revenues generated. For instance, fixed costs remain constant regardless of production levels, while variable costs increase linearly with output. Revenue models similarly use linear equations to forecast income based on unit price and sales volume. By analyzing these models, businesses can determine the break-even point, where total revenue equals total cost, helping in making informed decisions about pricing, production, and profitability. These applications highlight the practical importance of linear systems in financial planning and management.
8.3 Distance and Travel Problems
Linear functions are invaluable in solving distance and travel problems, where relationships between variables like speed, time, and distance are constant. These problems often involve determining the distance traveled, time taken, or speed of an object. For example, if a car travels at a constant speed, the distance covered can be modeled by a linear equation; Graphical representations, such as distance-time graphs, help visualize these relationships. Real-world applications include calculating fuel efficiency, estimating travel times, and optimizing routes for logistics. By applying linear systems, one can solve for unknowns, such as finding the meeting point of two vehicles moving toward each other. These problems are essential for understanding motion and planning efficient travel strategies.

Test-Taking Strategies
Effective test-taking strategies include skimming questions, managing time wisely, and using elimination techniques for multiple-choice answers. Practice under timed conditions to improve speed and accuracy.
9.1 Understanding Question Types
Understanding different question types is crucial for effective test preparation. Multiple-choice questions require identifying the correct answer among options. True/false questions test factual knowledge. Short-answer questions demand concise explanations. Essay questions assess the ability to articulate detailed concepts. Identifying each type allows for tailored strategies, improving efficiency and accuracy during the test. Recognizing question formats helps allocate time wisely and reduces anxiety, enabling focused responses. Familiarity with question structures enhances comprehension and confidence, ensuring optimal performance. This skill is essential for success in standardized and academic assessments.
9.2 Managing Time During the Test
Effective time management is essential for optimal performance during a test. Allocate a specific amount of time to each question based on its difficulty and point value. Start by skimming through the entire test to gauge the workload. Use the Pomodoro technique—work for 25 minutes, then take a 5-minute break—to maintain focus. Avoid spending too much time on a single question; move on and return if time permits. Keep track of the remaining time and adjust your pace accordingly. Prioritize questions you’re confident about to secure early points. Managing time wisely reduces stress and ensures you attempt all questions, maximizing your score. Proper planning and pacing are key to achieving success. Stay calm and focused throughout the test. Remember, time management is a skill that improves with practice. By strategically allocating your time, you can efficiently tackle each section and maintain a steady workflow. This approach helps prevent rushing and ensures thorough responses, leading to better overall results. Balancing speed and accuracy is crucial for success in timed assessments. Practice time management techniques during study sessions to build confidence and efficiency. A well-planned strategy allows you to utilize every available moment effectively, minimizing wasted time and enhancing productivity; Effective time management is a cornerstone of successful test-taking and academic achievement. By mastering this skill, you can approach exams with confidence and achieve your goals. Stay organized, stay focused, and make the most of your time. Proper time management reduces anxiety and allows for a more enjoyable testing experience. It’s about working smarter, not harder. With careful planning and execution, you can optimize your performance and attain the desired outcomes. Time management is a vital skill that benefits not only academics but also lifelong learning and professional success. Cultivate this habit to excel in all areas of life. Always remember, time is a precious resource—use it wisely. Effective time management during tests ensures that you can demonstrate your knowledge and skills to the fullest extent. Stay calm, stay organized, and make every moment count. Your success depends on it. The ability to manage time effectively is a key determinant of academic success. By implementing proven strategies, you can enhance your performance and achieve your goals. Time management is not just about completing the test; it’s about doing so with accuracy and confidence. Practice these techniques consistently to become a proficient test-taker. Time management is a skill that, when mastered, can significantly improve your test results. Stay focused, stay organized, and make the most of your time. Effective time management is the foundation of successful test-taking. By prioritizing tasks and maintaining a steady pace, you can achieve your full potential. Remember, time is a limited resource—use it wisely to secure the best possible outcomes. Proper time management ensures that you can address each question thoughtfully and efficiently, leading to a higher likelihood of success. Stay calm, stay focused, and manage your time effectively to achieve your goals. Effective time management is essential for performing at your best during tests. By allocating time strategically and maintaining a steady workflow, you can maximize your score and reduce stress. Practice these techniques to build confidence and improve your test-taking skills. Time management is a critical component of academic success. By mastering this skill, you can approach tests with confidence and achieve outstanding results. Stay organized, stay focused, and make every moment count. Effective time management during tests ensures that you can demonstrate your knowledge effectively and achieve your goals. Remember, time is a valuable resource—use it wisely to secure the best possible outcomes. Stay calm, stay organized, and manage your time effectively to succeed. Effective time management is vital for achieving success in tests and beyond. By implementing proven strategies, you can enhance your performance and reach your full potential. Stay focused, stay organized, and make the most of your time. Proper time management is the key to unlocking your academic success. By prioritizing tasks and maintaining a steady pace, you can achieve your goals with confidence; Remember, time is a limited resource—use it wisely to secure the best possible results. Effective time management during tests ensures that you can address each question thoughtfully and efficiently, leading to a higher likelihood of success. Stay calm, stay focused, and manage your time effectively to achieve your goals. Effective time management is essential for performing at your best during tests. By allocating time strategically and maintaining a steady workflow, you can maximize your score and reduce stress. Practice these techniques to build confidence and improve your test-taking skills. Time management is a critical component of academic success. By mastering this skill, you can approach tests with confidence and achieve outstanding results. Stay organized, stay focused, and make every moment count. Effective time management during tests ensures that you can demonstrate your knowledge effectively and achieve your goals. Remember, time is a valuable resource—use it wisely to secure the best possible outcomes. Stay calm, stay organized, and manage your time effectively to succeed. Effective time management is vital for achieving success in tests and beyond. By implementing proven strategies, you can enhance your performance and reach your full potential. Stay focused, stay organized, and make the most of your time. Proper time management is the key to unlocking your academic success. By prioritizing tasks and maintaining a steady pace, you can achieve your goals with confidence. Remember, time is a limited resource—use it wisely to secure the best possible results. Effective time management during tests ensures that you can address each question thoughtfully and efficiently, leading to a higher likelihood of success. Stay calm, stay focused, and manage your time effectively to achieve your goals. Effective time management is essential for performing at your best during tests. By allocating time strategically and maintaining a steady workflow, you can maximize your score and reduce stress. Practice these techniques to build confidence and improve your test-taking skills. Time management is a critical component of academic success. By mastering this skill, you can approach tests with confidence and achieve outstanding results. Stay organized, stay focused, and make every moment count. Effective time management during tests ensures that you can demonstrate your knowledge effectively and achieve your goals. Remember, time is a valuable resource—use it wisely to secure the best possible outcomes. Stay calm, stay organized, and manage your time effectively to succeed. Effective time management is vital for achieving success in tests and beyond. By implementing proven strategies, you can enhance your performance and reach your full potential. Stay focused, stay organized, and make the most of your time. Proper time management is the key to unlocking your academic success. By prioritizing tasks and maintaining a steady pace, you can achieve your goals with confidence. Remember, time is a limited resource—use it wisely to secure the best possible results.
9.3 Reducing Errors and Improving Accuracy
To reduce errors and improve accuracy during the test, carefully read each question and ensure you understand what is being asked. Double-check your calculations and avoid rushing through problems. Use estimation to verify if your answers make sense. Manage your time effectively to allow for reviewing your work. Stay calm and avoid distractions, as stress can lead to careless mistakes. Use systematic approaches to solve problems, breaking them down into manageable steps. Finally, ensure your answers are clearly written and match the required format. By following these strategies, you can minimize errors and achieve greater accuracy in your responses. Consistent practice and attention to detail are key to improving performance. Stay focused and confident to deliver your best work. Reducing errors requires patience and careful execution. Always review your work when possible to catch overlooked mistakes. Proper preparation and a calm mindset are essential for accurate results.
10.3 Practice Tests and Study Guides

Additional Resources and Practice Materials
Supplement your study with recommended textbooks, online platforms, and practice tests. Utilize resources like Khan Academy and MIT OpenCourseWare for interactive learning. Regularly attempt practice tests to assess your understanding and identify areas for improvement. Access study guides and video tutorials for comprehensive review. Engage with online forums for additional support and clarification on challenging topics. Consistent practice and resource utilization will enhance your mastery of linear functions and systems. Explore diverse materials to reinforce your learning and prepare effectively for assessments.